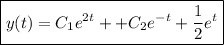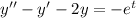
The corresponding homogeneous ODE is
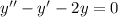
with characteristic equation
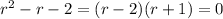
with roots at
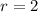 and
and
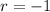 , so the characteristic solution is
, so the characteristic solution is
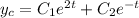
For the non-homogeneous ODE, assume a particular solution of the form
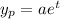
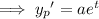
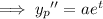
Substituting
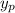 and its derivatives into the ODE gives
and its derivatives into the ODE gives
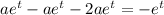
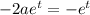
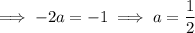
Then the ODE has the general solution