Explanation:
In the attached images we can see the rigid transformation of the function
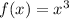
1. The basic graph
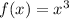
2. The reflected graph
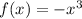
3. The displaced graph
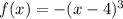
Reflection: In the expression
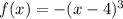 , the sign - before the parenthesis indicates that the function is reflected in the x axis, for this case the function is even, this means that -f(x) = f(-x) , then the reflection on the x axis is equal to the reflection on the y axis.
, the sign - before the parenthesis indicates that the function is reflected in the x axis, for this case the function is even, this means that -f(x) = f(-x) , then the reflection on the x axis is equal to the reflection on the y axis.
Displacement: We observe the term (x-4) of the function
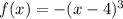 and analyze the value -4, where, the sign - indicates displacement to the right and the value 4 indicates the amount that the graph shifted .
and analyze the value -4, where, the sign - indicates displacement to the right and the value 4 indicates the amount that the graph shifted .