Question

Modulus of resilience is: (a) Slope of elastic portion of stress- strain curve (b) Area under the elastic portion of the stress-strain curve (c) Energy absorbed during fracture in a tension test (d) Energy absorbed during fracture in an impact test (e) Slope of the plastic portion of the stress- strain curve

Answer 1

Answer: b) Area under the elastic portion of the stress-strain curve

Explanation:

By definition, resilience is the strain-energy density stored by the material when it is stressed to the proportional limit defined by Hooke's Law. Resilience is given by the following expression:

μ(r) =
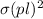`\sigma(pl)^(2)` / 2E

μ(r) is the modulus of resilience

σ(pl) is the stress to the proportional limit

E is the elastic modulus

When you look at the stress-strain curve, the area under the elastic portion (up to the proportional limit) can be obtained by the area of a triangle with base equal to the strain (σ) and height equal to the stress (ε):

Ω = (b . h) / 2 = (σ(pl) . ε) / 2

Using Hooke's Law: σ = E . ε → ε = σ/E

Replacing the expression in the area equation:

Ω = (σ(pl) . ε) / 2 =
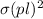`\sigma(pl)^(2)` / 2E = μ(r)