Question

Find the value of x in the isosceles triangle

Answer 1

That is a question about triangles.

In my answer I will show 2 ways to solve that question, ok? Let's go.

First way - Pythagoras's theorem

The line segment x divide the biggest triangle in 2 equals right triangles.

Let's choose one of them and note that is a triangule with hypotenuse equals to 8 and one cathetus equals to half of 8.

The Pythagoras's theorem says that:

`\boxed{a^2 = b^2 + c^2}`

a is the hypotenuse and b and c are cathetus.

So, in our case, we know the hypotenuse and one cathetus, let's substitute that in the expression:

`a^2 = b^2 + c^2\\8^2 = 4^4 + c^2\\64 = 16 + c^2\\c^2 = 64 - 16\\c^2 = 64 -16\\c^2 = 48\\c = √(48)\\c= 4√(3)`

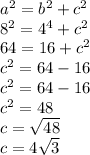
Therefore, the value of x is
`4√(3)`.

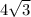Second way - The equilateral triangle height

That way to solve the question is a consequence of the previous way.

That triangle has all the sides equals, so it is a equilateral triangle.The line segment x is the height of that triangle. And we can find the equilateral triangle height using that expression:

`\boxed{h = (S\cdot √(3) )/(2) }`

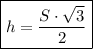
h is the height and S is the triangle's side.

So, we know that the side of our triangle is 8. Let's change S value in the expression:

`h = (S\cdot √(3) )/(2) \\h = (8\cdot √(3) )/(3) \\h = 4√(3)`

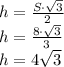
Thus, the value of x is
`4√(3)`.

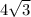Note that in the 2 ways we find the same result, so that answer is correct.

I hope I've helped. :D

Enjoy your studies! \o/

Answer 2

Explanation:

Since all 3 sides of the triangle is equal, it is not only an isosceles, but an equilateral triangle.

x = 8sin60° = 6.928 or sqrt48.