Answer: 0.336 m
Step-by-step explanation:
This situation is a good example of the parabolic motion, in which the travel of the squirrel has two components: x-component and y-component. Being their main equations as follows:
x-component:
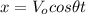 (1)
(1)
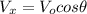 (2)
(2)
Where:
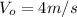 is the squirrel's initial speed
is the squirrel's initial speed
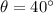 is the angle at which the squirrel jumps into the air
is the angle at which the squirrel jumps into the air
 is the time since the bullet is shot until it hits the ground
is the time since the bullet is shot until it hits the ground
y-component:
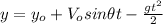 (3)
(3)
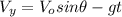 (4)
(4)
Where:
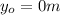 is the initial height of the squirrel
is the initial height of the squirrel
 is the final height of the squirrel (when it finally hits the ground)
is the final height of the squirrel (when it finally hits the ground)
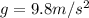 is the acceleration due gravity
is the acceleration due gravity
Now, we have to find the maximum height
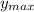 reached by the squirrel, and this happens when
reached by the squirrel, and this happens when
 . So equation (2) is rewritten as:
. So equation (2) is rewritten as:
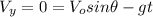 (5)
(5)
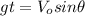 (6)
(6)
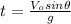 (7)
(7)
Solving (7):
 (8)
(8)
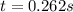 (9)
(9)
Substituting the value of
 (9) in (3):
(9) in (3):
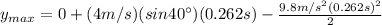 (10)
(10)
Finally:
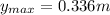 (11)
(11)