Question

What is the average rate of change of the function g(x) = 3(2^x) - 6 over the interval [0,3]? Show all work.

Answer 1

7

Explanation:

The average rate of change here, since this is not a line, is the slope of the secant line that is connecting those 2 points. We can find that average rate of change by finding the y coordinates that go with each of those x coordinates and then applying the slope formula. For g(0):

`g(0)=3(2)^0-6`

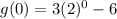
Anything raised to the power of 0 is 1, so we have then:

g(0) = 3(1) - 6 so

g(0) = -3 and the coordinate pair is (0, -3)

For g(3):

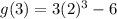`g(3)=3(2)^3-6` so

g(3) = 18 and the coordinate pair is (3, 18).

Now we plug those into the slope formula:

`m=(18-(-3))/(3-0)=7`

So the averagee rate of change, which is also the slope, between those 2 points is 7