Answer:
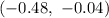
Explanation:
The confidence interval for the difference of two population proportion is given by :-
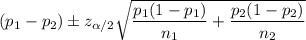
Given : The first sample consists of 20 people with 9 having a common attribute.
Here,
 ,
,
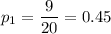
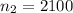 ,
,
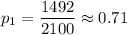
Significance level :

Critical value :
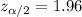
A 95% confidence interval for the difference of two population proportion will be :-
