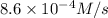Question

The following data is given to you about a reaction you are studying: Overall reaction: 2A  D Proposed mechanism: Step 1 A + B  C (slow) Step 2 C + A  D + B (fast) [A]o = 0.500 M [B]o = 0.0500 M [C]o = 0.500 M [D]o = 1.50 M This reaction was run at a series of temperatures and it was found that a plot of ln(k) vs 1/T (K) gives a straight line with a slope of -982.7 and a Y intercept of -0.0726. What is the initial rate of the reaction at 298K?

Answer 1

Answer : The initial rate of the reaction at 298 K is,
`8.6* 10^(-4)M/s`

Explanation :

The Arrhenius equation is written as:

`K=A* e^{(-Ea)/(RT)}`

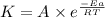
Taking logarithm on both the sides, we get:

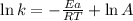`\ln k=-(Ea)/(RT)+\ln A` ............(1)

where,

k = rate constant

Ea = activation energy

T = temperature

R = gas constant = 8.314 J/K.mole

A = pre-exponential factor

The equation (1) is of the form of, y = mx + c i.e, the equation of a straight line.

Thus, if we plot a graph of
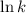`\ln k` vs
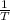`(1)/(T)` then the graph shows a straight line with negative slope. That means,

Slope of the line =
`-(Ea)/(R)`

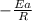
And,

Intercept =
`\ln A`

As we are given that:

Slope of the line = -982.7 =
`-(Ea)/(R)`

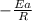
Intercept = -0.0726 =
`\ln A`

Now we have to calculate the value of rate constant by putting the value of slope, intercept and temperature (298K) in equation 1, we get:

`\ln k=-(982.7)/(298)+(-0.0726)`

`\ln k=-3.37`

`k=0.0344s^(-1)`

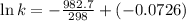
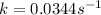
The value of rate constant is,
`0.0344s^(-1)`

Now we have to calculate the initial rate of the reaction at 298 K.

As we know that the slow step is the rate determining step. So,

The slow step reaction is,

`A+B\rightarrow C`

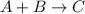
The expression of rate law for this reaction will be,

`Rate=k[A][B]`

As we are given that:

[A] = 0.500 M

[B] = 0.0500 M

k =
`0.0344s^(-1)`

Now put all the given values in the rate law expression, we get:

`Rate=(0.0344)* (0.500)* (0.0500)`

`Rate= 8.6* 10^(-4)M/s`

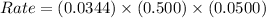
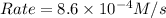
Therefore, the initial rate of the reaction at 298 K is,
`8.6* 10^(-4)M/s`