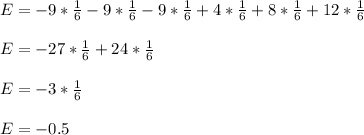Question

While at a carnival, Andrew comes across a game that involves rolling a die. According to the game's rules, if the number rolled is even, the player wins dollars equivalent to two times the number. And if the number rolled is odd, the player loses $9. If Andrew rolls the die once, he can expect to win or lose? .5$? or a 1.5$?

Answer 1

Answer: he can expect to lose 0.5$

Explanation:

Answer 2

he can expect to lose 0.5$

Explanation:

To solve this problem we must calculate the expected value of the game.

If x is a discrete random variable that represents the gain obtained when rolling a dice, then the expected value E is:

`E =\sum xP (x)`

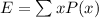
When throwing a dice the possible values are:

x: 1→ -$9; 2→ $4; 3→ -$9; 4→ $8; 5→ -$9; 6→ $12

The probability of obtaining any of these numbers is:

`p=(1)/(6)`

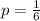
The gain when obtaining an even number is twice the number.

The loss to get an odd number is $ 9

So the expected gain is:

`E=-9*(1)/(6)-9*(1)/(6)-9*(1)/(6) + 4*(1)/(6) + 8*(1)/(6) + 12*(1)/(6)\\\\E =-27*(1)/(6) + 24*(1)/(6)\\\\E=-3*(1)/(6)\\\\E=-$0.5`