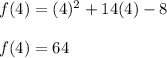Question

PLEASE HELP!!! What is the remainder when f(x) = x2 + 14x − 8 is divided by (x − 4)?

Answer 1

64.

Explanation:

The Remainder Theorem states that if (x - a) is a factor of f(x) then f(a) is a remainder when f(x) is divided by (x - a.)

So here, by the Remainder Theorem the remainder will be f(4).

So it is = (4)^2 + 14(4) - 8

= 16 + 56 - 8

= 72 - 8

= 64.

Answer 2

Answer: The remainder is 64.

Explanation:

By definition, when we divide a polynomial f(x) by
`(x-a)` the remainder will be:

`f(a)`

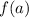
In this case we know that f(x) is:

`f(x) = x^2 + 14x -8`

And we need to find the remainder when it is divided by
`(x -4)`.

Therefore, substituting
`x=4` into f(x), we get that the remainder is:
`f(4) = (4)^2 + 14(4) -8\\\\f(4)=64`