Answer:
Cyclist A travels at 11 km/hr and cyclist B travels at 16 km/r
Step by step explanation:
The cyclist B is riding 5 km/hr faster than cyclist A. From 09:00 till 10:45 is 1 hour and 45 minutes. This is 60 plus 45 minutes:
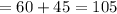
In 105 minutes they are 47.25 km apart. Let x be the speed of cyclist A and y be the speed of cyclist B. We can write x in terms of y:
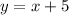
We can write an expression relating the two cyclists to the total speed of the cyclists.
We know that in 105 minutes they are 47.25 km apart.
We can substitute the 47.25 km into the following expression:
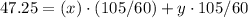
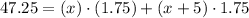
Solve for x
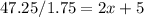
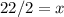
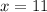
Therefore y is:
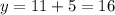
Cyclist A travels at 11 km/hr and cyclist B travels at 16km/r