Question

At 9:00 on Saturday morning, two bicyclists heading in opposite directions pass each other on a bicycle path.The bicyclist heading north is riding 5 km/hour faster than the bicyclist heading south. At 10:45, they are 47.25 km apart. Find the two bicyclists’ rates.

Answer 1

Between 9:00 am and 10:45 am, there have been 1 hour and 45 minutes or 1.75 hours have passed. Let x be the speed of the slower cyclist and x+ 5 be the rate of the second cyclist. The given situation is best represented through the equation below,

x(1.75) + (x + 5)(1.75) = 47.25 km

The value of x from the equation is 11. Thus, the two bicyclists' rates are 11 km/h and 16 km/h.

Answer 2

Cyclist A travels at 11 km/hr and cyclist B travels at 16 km/r

Step by step explanation:

The cyclist B is riding 5 km/hr faster than cyclist A. From 09:00 till 10:45 is 1 hour and 45 minutes. This is 60 plus 45 minutes:

`=60+45=105`

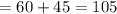
In 105 minutes they are 47.25 km apart. Let x be the speed of cyclist A and y be the speed of cyclist B. We can write x in terms of y:

`y=x+5`

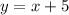
We can write an expression relating the two cyclists to the total speed of the cyclists.

We know that in 105 minutes they are 47.25 km apart.

We can substitute the 47.25 km into the following expression:

`47.25=(x)\cdot(105/60)+y\cdot{105/60}`

`47.25=(x)\cdot(1.75)+(x+5)\cdot{1.75}`

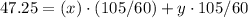
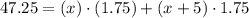
Solve for x

`47.25/1.75=2x+5`

`22/2=x`

`x=11`

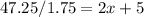
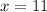
Therefore y is:

`y=11+5=16`

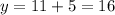
Cyclist A travels at 11 km/hr and cyclist B travels at 16km/r