Question

A sample of 80 women is​ obtained, and their heights​ (in inches) and pulse rates​ (in beats per​ minute) are measured. The linear correlation coefficient is 0.284 and the equation of the regression line is ModifyingAbove y with caret equals 17.8 plus 0.920 x​, where x represents height. The mean of the 80 heights is 63.1 in and the mean of the 80 pulse rates is 75.9 beats per minute. Find the best predicted pulse rate of a woman who is 68 in tall. Use a significance level of alpha equals 0.05.

Answer 1

80.36 beats per minute

Explanation:

Given data in the problem:

Equation for the regression line is given in the problem as:

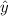`\hat{y}` = 17.8 + 0.920x

where,

'x' is the height

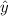`\hat{y}` is the pulse rate

now, for calculating the best predicted pulse rate of a 68 in tall women

substitute x = 68" the regression equation provided, we get

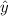`\hat{y}` = 17.8 + (0.920 × 68)

or

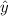`\hat{y}` = 80.36 beats per minute