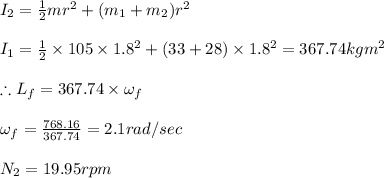Question

Three children are riding on the edge of a merry‑go‑round that has a mass of 105 kg105 kg and a radius of 1.80 m1.80 m . The merry‑go‑round is spinning at 16.0 rpm.16.0 rpm. The children have masses of 22.0,22.0, 28.0,28.0, and 33.0 kg.33.0 kg. If the 28.0 kg28.0 kg child moves to the center of the merry‑go‑round, what is the new angular velocity in revolutions per minute? Ignore friction, and assume that the merry‑go‑round can be treated as a solid disk and the children as point masses.

Answer 1

New angular speed changes from 16 rpm to 19.95 rpm

Step-by-step explanation:

In the given system the angular momentum of the system is conserved

initial angular momentum of the system

`L_(i)=I_(1)\omega _(1)\\\\\omega _(1)=(8\pi )/(15)rad/sec\\\\I_(1)=(1)/(2)mr^(2)+(m_(1)+m_(2)+m_(3))r^(2)\\\\I_(1)=(1)/(2)* 105* 1.8^(2)+(33+28+28) * 1.8^(2)=458.46kgm^(2)\\\\\therefore L_(i)=458.46* (8\pi )/(15)=768.16`

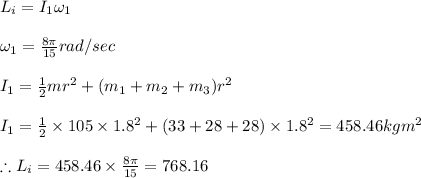
When 28 kg child moves to the center the moment of inertia changes thus we have

`I_(2)=(1)/(2)mr^(2)+(m_(1)+m_(2))r^(2)\\\\I_(1)=(1)/(2)* 105* 1.8^(2)+(33+28) * 1.8^(2)=367.74kgm^(2)\\\\\therefore L_(f)=367.74* \omega _(f)`

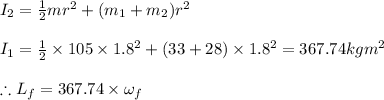
Equating initial and final angular momentum we get

`I_(2)=(1)/(2)mr^(2)+(m_(1)+m_(2))r^(2)\\\\I_(1)=(1)/(2)* 105* 1.8^(2)+(33+28) * 1.8^(2)=367.74kgm^(2)\\\\\therefore L_(f)=367.74* \omega _(f)\\\\\omega _(f)=(768.16)/(367.74)=2.1rad/sec\\\\N_(2)=19.95rpm`