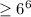Question

Tom says that he needs 6 rolls to obtain each possible outcome on a 6-sided die. On the fourth roll, he rolls his second "3". Tom says that the die is loaded and that each outcome is not equally likely. Is Tom correct here? If you think Tom is incorrect, how many rolls should Tom make until he sees each number occurring about 1/6 of the time?

Answer 1

Tom is incorrect

Explanation:

The odds of getting any number on a 6-sided die are
`1:6`

Every time he rolls, there is a
`1:6` chance he gets any number. Therefore, it is totally plausible to get the same number again. As the number of rolls tends toward infinity, the ratio of each number occurring to number of rolls equals
`1:6`.

Answer 2

Answer with explanation:

Number of Possible Outcome when you roll a 6 faced die ={1,2,3,4,5,6}

Probability of each Outcome

`=(1)/(6)`

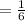
Tom's Statement

1.→He Says that, he needs 6 rolls to obtain each possible outcome on a 6-sided die.

2.→On the fourth roll, he rolls his second "3".

3.→Tom says that the die is loaded and that each outcome is not equally likely.

→All the three statements are Incorrect.As the number of trials increases , the chances of occuring of each event equally increases.

→Number of rolls should Tom make until he sees each number occurring about
`(1)/(6)` of the time approximately

`\geq 6^6`