Question

If $4200 is invested in a savings account for which interest is compounded

semiannually, and if the $4200 turns into $4900 in 4 years, what is the interest
rate of the savings account?

Answer 1

3.9%

Explanation:

The formula for compound interest to apply is;

`A=P(1+(r)/(n) )^(nt)`

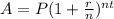
where;

A=amount at the end

P=starting amount/principal

n=number of compounding years

t=total number of years

r=interest rate expressed as a decimal

Given

P=$4200, n=2, t=4 and A=$4900 R=?

Substitute values in equation, take r=r

`A=P(1+(r)/(n) )^(nt) \\\\\\4900=4200(1+(r)/(2) )^(2*4) \\\\\\4900=4200(1+0.5r)^8`

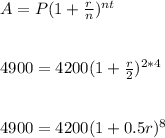
Divide both sides by 4200

`(4900)/(4200) =(4200)/(4200) (1+0.5r)^8\\\\\\1.1667=(1+0.5r)^8`

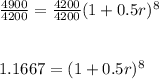
Introduce root 8 to the left hand side, thus eliminating the power 8 in the right hand side

`\sqrt[8]{1.1667} =1+0.5r\\\\\\1.0195=1+0.5r\\\\\\1.0195-1=0.5r\\\\\\0.0195=0.5r\\\\\\(0.0195)/(0.5) =(0.5r)/(0.5) \\\\\\0.039=r`

r=3.9%