Answer:
The amount of energy generate by the generators if they work simultaneously for 40 minutes is 1/2.
Explanation:
Consider the provided information.
One of the generators produces n units of energy in 4 hours, and the other generator produces the same amount of energy in half the time.
Let the total hours = n
The first generator produces energy in 1 hr = n/4
The first generator produces energy in 1 hr = n/2
Total energy is:
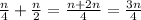
Total time taken is 40 mins. Now convert 40 minutes into hours:
40/60 = 2/3 hr
Now to find the amount of energy generate by the generators if they work simultaneously for 40 minutes is:
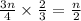
Hence, the amount of energy generate by the generators if they work simultaneously for 40 minutes is 1/2.