Answer:
$29364.95
Explanation:
The formula to apply is;
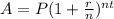
where ;
A=amount at the end
P=principal amount
r=rate of interest as a decimal
n=number of compoundings a year
t=total number of years
Given in the question
A=$55000
t=8 years
n=2
r=0.08
P=?
Substitute the values in the equation;
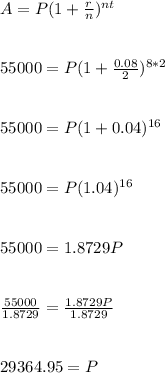
Checking the answer
