Step-by-step explanation:
Since, the given reaction is
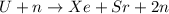
Sum of masses on both reactant and product side is as follows.
235.043924 + 1.008665 = 139.921620 + 93.915367 + (2 × 1.008665)
= 0.198272 u
As it is known that relation between energy and mass is as follows.
Energy produced =
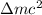
Since, 1 u = 931.494 MeV/
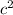 . Putting this value into the above formula as follows.
. Putting this value into the above formula as follows.
Energy produced =
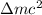
=
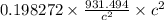
= 184.69 MeV
As 1 MeV equals
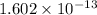 joules.
joules.
Hence, 184.69 MeV will be converted into joules as follows.
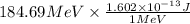
=
 J
J
=
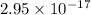 J
J
Thus, we can conclude that energy released in this reaction is
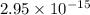 J.
J.