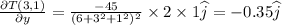Question

The temperature at a point (x, y) on a flat metal plate is given by T(x, y) = 45/(6 + x2 + y2), where T is measured in °C and x, y in meters. Find the rate of change of temperature with respect to distance at the point (3, 1) in the x-direction and the y-direction. (a) the x-direction °C/m (b) the y-direction °C/m

Answer 1

Change in x direction is
`-1.054^(o)C`

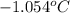
Change in y direction is
`-0.35^(o)C`

Step-by-step explanation:

The temperature is given by we need to find gradient of temperature to obtain the rate of change thus

`T(x,y)=(45)/(6+x^(2)+y^(2))\\\\\therefore \bigtriangledown T(x,y)=(\partial T(x,y))/(\partial x) \widehat{i}+(\partial T(x,y))/(\partial y) \widehat{j}\\\\(\partial T(x,y))/(\partial x)=(-45)/((6+x^(2)+y^(2))^(2))* 2x\widehat{i}\\\\(\partial T(x,y))/(\partial y)=(-45)/((6+x^(2)+y^(2))^(2))* 2y\widehat{j}\\\\`

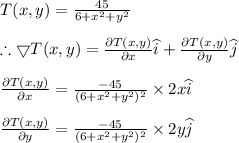
Now the rate of change at (3,1) in

1) X direction is given by

`(\partial T(3,1))/(\partial x)=(-45)/((6+3^(2)+1^(2))^(2))* 2* 3\widehat{i}=-1.054\widehat{i}`

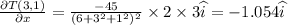
2) Y direction is given by

`(\partial T(3,1))/(\partial y)=(-45)/((6+3^(2)+1^(2))^(2))* 2* 1\widehat{j}=-0.35\widehat{j}\\\\`