Question

Determine which set of numbers can be the measures of the sides of a triangle.

Question 6 options:

a)

13, 10, 16

b)

1, 2, 3

c)

5.2, 11, 4.9

d)

208, 9, 219

Answer 1

Option A) 13, 10, 16

Explanation:

We are given the following information in the question:

The triangular Inequality:

• The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
• 
  `\text{Side 1} + \text{Side 2} > \text{Side 3}`

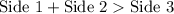
a) 13, 10, 16

`13 + 10 = 23 > 16`

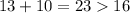
Thus, they can be the measures of the sides of a triangle.

b) 1, 2, 3

`1 + 2 = 3 \\gtr 3`

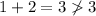
Thus, they cannot be the measures of the sides of a triangle as they do not satisfy the triangular inequality.

c) 5.2, 11, 4.9

`5.2 + 4.9 = 10.1 \\gtr 11`

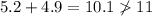
Thus, they cannot be the measures of the sides of a triangle as they do not satisfy the triangular inequality.

d) 208, 9, 219

`208 + 9 = 217 \\gtr 219`

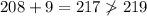
Thus, they cannot be the measures of the sides of a triangle as they do not satisfy the triangular inequality.

Answer 2

a) 13, 10, 16

Explanation:

The usual form of the triangle inequality requires the sum of the two shortest sides exceed the longest side (a+b>c). The only choice for which this is true is ...

10 + 13 > 16 . . . . choice A

_____

Comment on the triangle inequality

Some authors also allow the sum to equal the longest side (a+b≥c). In that case, choice B (1+2=3) is also an answer. This "triangle" would look like a line segment of length 3. It has zero area.