Question

A dog chasing a rabbit, rabbit runs 60 leaps before the dog. When the dog jumps 2 leaps rabbit can jumps 3 leaps. But rabbit have to jump 7 leaps to cover the distance that dog cover by 3 leaps. How many leaps that the dog jumps when rabbit and dog meet?

Answer 1

x=vel of d

y=vel oh h

t1=time taken by d

t2=time taken by h

we have 4t1=5t2..............(1)

also

3xt1=4yt2....................(2)

comparing 1 and 2

x/y=16/15

Explanation:

Answer 2

72 leaps

Explanation:

Given: A dog chasing a rabbit, rabbit runs 60 leaps before the dog. When the dog jumps 2 leaps rabbit can jumps 3 leaps. But rabbit have to jump 7 leaps to cover the distance that dog cover by 3 leaps.

To Find: number of leaps that the dog jumps when rabbit and dog meet.

Solution:

Let the units of leaps jumped by rabbit be r

Let the units of leaps jumped by dog be d

7 leaps of rabbit =3 leaps of dog

`7\text{r}=3\text{d}`

`1\text{r}=(3)/(7)\text{d}`

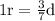
rabbit runs 60 leaps before the dog,

therefore

distance between dog and rabbit=60r=
`60*(3)/(7)\text{d}`

When the dog jumps 2 leaps rabbit can jump 3 leaps

speed of rabbit(
`\text{S}_(r)`)=
`3\text{r}`=
`3*(3)/(7)\text{d}`

`(9)/(7)\text{d}`

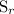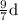
speed of dog(
`\text{S}_(d)`) =
`2\text{d}`

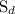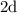
As dog and rabbit are running is same direction,

relative speed of dog and rabbit (
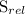`\text{S}_(rel)`)=speed of dog-speed of rabbit

(
`\text{S}_(d)`)-(
`\text{S}_(r)`)

`2\text{d}-(9)/(7)\text{d}`

`(5)/(7)\text{d}`

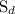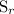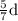
the distance to be covered by dog before catching rabbit

`60\text{r}`

`(3)/(7)*60\text{d}`

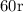
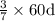
Now,

`\text{time}=\frac{\text{distance}}{\text{speed}}`

`\text{time}=\frac{(3)/(7)*60\text{d}}{(5)/(7)\text{d}}`

`\text{time}=36\text{units}`

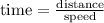
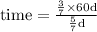
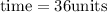
leaps jumped by dog in
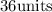`36\text{units}` of time

`2*36=72\text{leaps}`

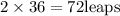
Hence the leaps jumped by dog when dog and rabbit meet are 72