Question

The population of a colony of mosquitoes obeys the law of uninhibited growth. If there are 1000 mosquitoes initially and there are 1700 after 1​ day, what is the size of the colony after 4 ​days? How long is it until there are 70,000 ​mosquitoes?

Answer 1

The size of the colony after 4 ​days is 8351.15.

8 days long there are 70,000 mosquitoes.

Explanation:

Given : The population of a colony of mosquitoes obeys the law of uninhibited growth. If there are 1000 mosquitoes initially and there are 1700 after 1​ day.

To find : What is the size of the colony after 4 ​days and How long is it until there are 70,000 ​mosquitoes?

Solution :

Let the uninhibited growth is defined by a function,

`A=A_0e^(kt)`

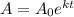
Where,
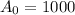`A_0=1000` is the initial amount

e is the Euler's constant

k is the amount of increase

t=1 day is the time

A=1700 is the amount

Substitute all the values in the formula,

`1700=1000e^(k(1))`

`(1700)/(1000)=e^(k(1))`

`1.7=e^(k)`

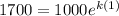
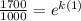
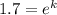
Taking natural log both side,

`\ln(1.7)=\ln(e^(k))`

`0.5306=k`

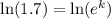
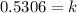
Now, The size of the colony after 4 ​days is

`A=1000e^((0.5306)(4))`

`A=1000e^(2.1224)`

`A=1000* 8.35115`

`A=8351.15`

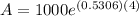
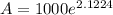
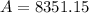
Therefore, The size of the colony after 4 ​days is 8351.15.

When there are 70,000 ​mosquitoes the time is

`70000=1000e^((0.5306)(t))`

`(70000)/(1000)=e^((0.5306)(t))`

`70=e^((0.5306)(t))`

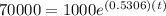
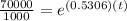
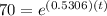
Taking ln both side,

`\ln(70)=\ln(e^(0.5306t))`

`4.248=0.5306t`

`t=(4.248)/(0.5306)`

`t=8`

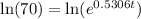
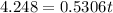
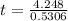
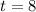
Therefore, 8 days long there are 70,000 mosquitoes.