Answer:
The size of the colony after 4 days is 8351.15.
8 days long there are 70,000 mosquitoes.
Explanation:
Given : The population of a colony of mosquitoes obeys the law of uninhibited growth. If there are 1000 mosquitoes initially and there are 1700 after 1 day.
To find : What is the size of the colony after 4 days and How long is it until there are 70,000 mosquitoes?
Solution :
Let the uninhibited growth is defined by a function,
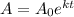
Where,
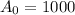 is the initial amount
is the initial amount
e is the Euler's constant
k is the amount of increase
t=1 day is the time
A=1700 is the amount
Substitute all the values in the formula,
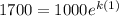
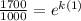
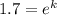
Taking natural log both side,
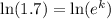
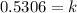
Now, The size of the colony after 4 days is
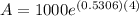
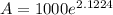
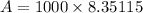
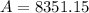
Therefore, The size of the colony after 4 days is 8351.15.
When there are 70,000 mosquitoes the time is
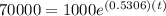
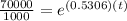
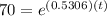
Taking ln both side,
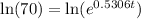
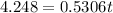
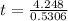
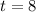
Therefore, 8 days long there are 70,000 mosquitoes.