Air compressed in car engine from 25 C and 100 kPa in reversible and adiabatic manner. If the compression ratio = 9.058, determine final temperature of air.

Question

asked Aug 26, 2020 141k views

1 Answer

Vince Gonzales · Answer 1 · 2020-09-02T03:31:07+0000

Step-by-step explanation:

It is given that,

Initial temperature,
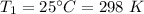
$T_1=25^(\circ)C=298\ K$

Pressure,
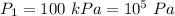
$P_1=100\ kPa=10^5\ Pa$

Compression ratio,
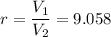
r=(V_1)/(V_2)=9.058

Let T₂ is the final temperature of air. Using the relation for reversible adiabatic process as :

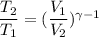$(T_2)/(T_1)=((V_1)/(V_2))^(\gamma-1)$ ............(1)

Where,

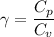
$\gamma=(C_p)/(C_v)$

For air,
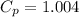C_p=1.004 and
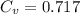
C_v=0.717

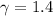
$\gamma=1.4$

So, equation (1) becomes :

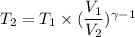
$T_2=T_1* ((V_1)/(V_2))^(\gamma-1)$

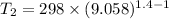
T_2=298* (9.058)^(1.4-1)

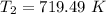
$T_2=719.49\ K$

So, the final temperature of air is 719.49 K. Hence, this is the required solution.