Question

Air at 1.3 bar, 500 K and a velocity of 40 m/s enters a nozzle operating at steady state and expands adiabatically to the exit, where the pressure is 0.85 bar and velocity is 250 m/s. For air modeled as an ideal gas with k = 1.4, determine for the nozzle: (a) the temperature at the exit, in K, and (b) the percent isentropic nozzle efficiency.

Answer 1

Given:

Pressure, P = 1.3 bar

Temperature, T = 500 K

velocity, v = 40 m/s

Pressure, P' = 0.85 bar

velocity, v' = 250 m/s

k = 1.4

Solution:

Now, we know that:

specific heat at constant pressure,
`C_(p) = 1.005 KJ/kgK`

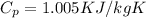
specific heat at constant volume,
`C_(p)` = 1.005 KJ/kgK

k =
`(C_(p))/(C_(V))`

(a) To calculate temperature at exit, T'

Using steady flow Eqn:

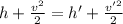`h + (v^(2))/(2) = h' + (v'^(2))/(2)` (1)

where

h = enthalpy =
`C_(p)T`

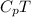
h'=
`C_(p)T'`

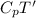
Now, from eqn (1)-

`h + (v^(2))/(2) = h' + (v'^(2))/(2)`

`C_(p)T + (v^(2))/(2) = C_(p)T' + (v'^(2))/(2)`

`1005* 500 + (40^(2))/(2) = 1005* T' + (v'^(2))/(2)`

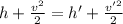
T' = 469.70 K

(b) To calculate % isentropic nozzle efficiency:

Using the relation:

`(T_(2s))/(T) = ((P')/(P))^(k - 1)/(k)`

⇒
`(T_(2s))/(500) = ((0.85)/(1.3))^(1.4 - 1)/(1.4)`

`{T_(2s) = 0.88 * 500 = 442.84 K`

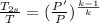
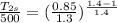
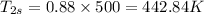
Now,

% isentropic nozzle efficiency,
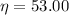`\eta =(T - T' )/(T - T_(2s))* 100`

%
`\eta =(500 - 469.70 )/(500 - 442.84)*100 = 53.00` %

`\eta = 53.00` %