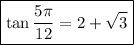Question

Exact value of tan 5pi/12

Answer 1

`\displaystyle \tan(5\pi)/(12)=2+√(3)`

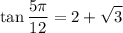
Explanation:

Tangent Half Angle

Given an angle θ, then:

`\displaystyle \tan {\frac {\theta }{2}}=\frac {\sin \theta }{1+\cos \theta}`

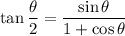
We are required to find:

`\tan(5\pi)/(12)`

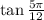
But it cannot be found in tables of main angles. We can use the angle

`\theta = (5\pi)/(6)`

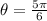
And use the formula above to find the required operation. Hence:

`\displaystyle \tan(5\pi)/(12)=\tan((5\pi)/(6))/(2)`

`\displaystyle \tan(5\pi)/(12)=\frac {\sin (5\pi)/(6) }{1+\cos (5\pi)/(6)}`

`\displaystyle \tan(5\pi)/(12)=\frac {(1)/(2) }{1-(√(3))/(2)}`

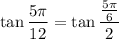
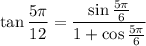
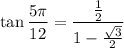
Operating:

`\displaystyle \tan(5\pi)/(12)=\frac {(1)/(2) }{(2-√(3))/(2)}`

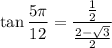
Simplifying:

`\displaystyle \tan(5\pi)/(12)=(1)/(2-√(3))`

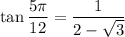
Rationalizing:

`\displaystyle \tan(5\pi)/(12)=(1)/(2-√(3))\cdot (2+√(3))/(2+√(3))`

`\displaystyle \tan(5\pi)/(12)=(2+√(3))/(2^2-√(3)^2)`

`\displaystyle \tan(5\pi)/(12)=(2+√(3))/(4-3)`

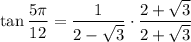
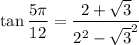
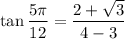
Finally:

`\boxed{\displaystyle \tan(5\pi)/(12)=2+√(3)}`