Question

A cola-dispensing machine is set to dispense a mean of 2.02 liters into a bottle labeled 2 liters. Actual quantities dispensed vary and the amounts are normally distributed with a standard deviation of 0.015 liters. a. What is the probability a bottle will contain between 2.00 and 2.03 liters? b. What is the probability a bottle will contain less than 2 liters? c. 2% of the containers will contain how much cola or more?

Answer 1

Explanation:

Given that a cola-dispensing machine is set to dispense a mean of 2.02 liters into a bottle labeled 2 liters.

Std deviation =0.015 litres

X- litres contained in a bottle is N(2.02, 0.15)

Z score is obtained as
`z=(x-2.02)/(0.015)`

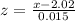
a) probability a bottle will contain between 2.00 and 2.03 liters

=P(2<x<2.03) = P(-1.33<Z<2)

= 0.4082+0.4772

=0.8854

b) P(X<2) = P(Z<-1.33) =0.5-0.4082 = 0.0918

c) 2% of containers

|z|<0.11

X lies between 0.6883 and 3.352 l