Answer:
weight will be greater by 20 gm.
Explanation:
to calculate the z score use negative z table for 0.14
P ( Z < x ) = 0.86
Value of z to the cumulative probability of 0.86 from normal table is 1.18
mean(μ) = 446 gm
standard deviation(σ) = 17 grams
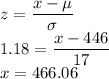
hence the weight will be greatest by
= 466 - 446 = 20 gm