Question

A wire of resistance R is cut into ten equal parts which are then connected in parallel. The equivalent resistance of the combination is

Answer 1

The equivalent resistance of the combination is R/100

Step-by-step explanation:

Parallel Connection of Resistances

If resistances R1, R2, R3,...., Rn are connected in parallel, the equivalent resistance is calculated as follows:

`\displaystyle (1)/(R_e)=(1)/(R_1)+(1)/(R_2)+(1)/(R_3)+...+(1)/(R_n)`

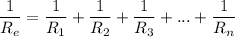
The electric resistance of a wire is directly proportional to its length. If a wire of resistance R is cut into 10 equal parts, then each part has a resistance of R/10.

It's known the 10 parts or resistance R/10 were connected in parallel, thus the electric resistance is:

`\displaystyle (1)/(R_e)=(1)/(R/10)+(1)/(R/10)+(1)/(R/10)+...+(1)/(R/10)`

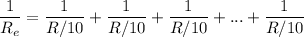
Note the sum consists of 10 equal terms. Operating on each term:

`\displaystyle (1)/(R_e)=(10)/(R)+(10)/(R)+(10)/(R)+...+(10)/(R)`

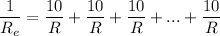
The sum of 10 identical fractions yields 10 times each fraction:

`\displaystyle (1)/(R_e)=10(10)/(R)=(100)/(R)`

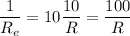
Solving for Re needs to take the reciprocal of both sides of the equation:

`R_e=R/100`

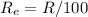
The equivalent resistance of the combination is R/100