Question

SAT Math Question (Thanks!)

f(x) = x^2 - 2x + 8
g(x) = -x^2 +18x +4

The two functions defined above are equal to each other when x=5+a or x=5-a, where a is a constant. What is the value of a?

Answer 1

`√(23)`.

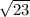Explanation:

So we are given the equations are equal for
`x=5\pm a`.

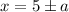If the functions are equal for those values then their difference is zero for those values:

`f-g=0`

`(x^2- 2x+8)-(-x^2 +18x +4)=0`

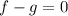
Combine like terms; keep in mind we are subtracting over the parenthesis:

`2x^2-20x+4=0`

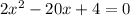
Since all terms have a common factor of 2, then divide both sides by 2:

`x^2-10x+2=0`

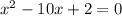
When compared to
`ax^2+bx+c=0` we should see:

`a=1`

`b=-10`

`c=2`

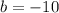
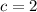
Now use quadratic formula.

`x=(-b \pm √(b^2-4ac))/(2a)`

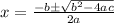
Plug in the values we found:

`x=(10 \pm √((-10)^2-4(1)(2)))/(2(1))`

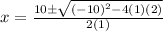
Let's simplify:

`x=(10 \pm √(100-8))/(2)`

`x=(10 \pm √(92))/(2)`

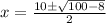
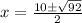
92 isn't a perfect square but contains a factor that is; 92=4(23):

`x=(10 \pm √(4) √(23))/(2)`

`x=(10 \pm 2√(23))/(2)`

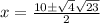
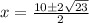
Divide top and bottom by since all three terms have a common factor 2:

`x=(10 \pm 2√(23))/(1)`

`x=5 \pm √(23)`

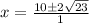
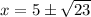
So f and g are equal for:

`x=5 \pm √(23)`

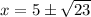
When compared to
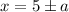`x=5\pm a` we see that
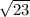`√(23)`.