Answer:
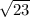 .
.
Explanation:
So we are given the equations are equal for
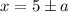 .
.
If the functions are equal for those values then their difference is zero for those values:
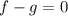
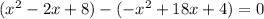
Combine like terms; keep in mind we are subtracting over the parenthesis:
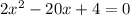
Since all terms have a common factor of 2, then divide both sides by 2:
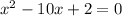
When compared to
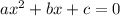 we should see:
we should see:
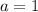
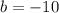
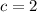
Now use quadratic formula.
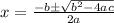
Plug in the values we found:
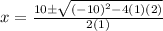
Let's simplify:
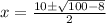
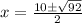
92 isn't a perfect square but contains a factor that is; 92=4(23):
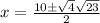
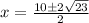
Divide top and bottom by since all three terms have a common factor 2:
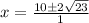
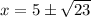
So f and g are equal for:
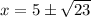
When compared to
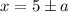 we see that
we see that
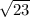 .
.