Question

Which statements are true about the graph of the function h(x) = -5x2 + 60x - 200? Select three options.

The axis of symmetry is the line x = -6.
The graph of h(x) will not intersect the graph of the parent function, f(x) = x2.
The vertex of the graph is at (6, -20).
The parabola has a maximum.
The value of k, when the equation is written in vertex form, is -200.

Answer 1

The given function is

h(x)=-5x²+60x-200

Let, h(x)=y

`y=-5* (x^2-12 x+40)\\\\ (y)/(-5)=(x-6)^2-36+40\\\\ (-y)/(5)-4=(x-6)^2\\\\y+20=-5(x-6)^2`

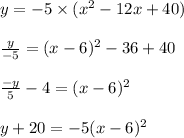
→The Vertex of the Parabola can be obtained by

x-6=0→x=6

And, y+20=0→y=-20

Vertex= (6,-20)

→Drawn the graph of Line, x=-6.

As,well as drawn the graph of , f(x)=x².

h'(x)=-10x+60

-10x+60=0

x=6

h"(x)=-10

Means Function attains maximum at , x=6.

→f(0)=-5×0²+60×0-200

= -200

→So, The value of k, when the equation is written in vertex form, is not -200.it will be , y= -20.

Correct Options are

B.→The graph of h(x) will not intersect the graph of the parent function, f(x) =x².

C.→ The vertex of the graph is at (6, -20).

D.→The parabola has a maximum.

Answer 2

B, C and D

Explanation:

The graph of the function h(x) is shown in attached diagram.

1. The vertex has coordinates:

`x_v=-(b)/(2a)=-(60)/(2\cdot (-5))=6\\ \\y_v=-5\cdot 6^2+60\cdot 6-200=-5\cdot 36+360-200=-180+160=-20.` Option C is true.

2. The axis of symmetry is vertical line which passes through the vertex, so its equation is x=6. Option A is false.

3. Since the graphs of the function h(x) and the parent function
`y=x^2` do not intersect, option B is true.

4. The parabola has a maximum - option D is true.

5. In vertex form, the equation is

`y=-5(x-6)^2-20`

Option E is false.