Question

Part of the graph of the function f(x) = (x - 1)(x + 7) is

shown below.
Which statements about the function are true? Select three options

Answer 1

The true ones:

V(-3,-16); the graph is increasing for x>-3; The graph is positive where x<-7 e and where x >1.

Explanation:

Distributing the factors, we'll have it expanded f(x)=x²+7x-x-7 ⇒ f(x)=x²+6x-7 in this form we can see the parameters a, b and c.

So the true statements are:

1)
`X_(v)=-((b)/(2a))\Rightarrow -((6)/(2))=X_(v)=-3\\Y_(v)=-((\Delta )/(4a))\Rightarrow -((36-4(1)(-7))/(4))=-16\\Vertex=(-3,-16)`

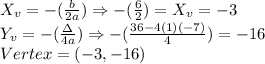
2) The Vertex indicates to us a change. At x< -3 the function, according to its graph was decreasing, then at x>-3, (-2,-1,0,1,..) the function increases.

3) Notice when x<-7, (x=-8, for example) the parabola is entirely over x-axis, then the graph for x <-7 is positive. And similarly, for x > 1, the function graph are over x-axis, then positive.

Answer 2

True: B, C and D

Explanation:

The graph of the function is shown in the attached diagram.

The vertex of the parabola (parabola is the graph of the function f(x)) is at (-3,-16), because

`x_v=(1+(-7))/(2)=-3\\ \\y_v=f(-3)=(-3-1)(-3+7)=-4\cdot 4=-16`

So, option A is false and option B is true.

As you can see from the graph, the function is increasing for all x>-3, thus option C is true.

The graph is positive for x<-7 and x>1 and negative for -7<x<1, so option D is true and option E is false.