Answer:
The true ones:
V(-3,-16); the graph is increasing for x>-3; The graph is positive where x<-7 e and where x >1.
Explanation:
Distributing the factors, we'll have it expanded f(x)=x²+7x-x-7 ⇒ f(x)=x²+6x-7 in this form we can see the parameters a, b and c.
So the true statements are:
1)
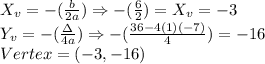
2) The Vertex indicates to us a change. At x< -3 the function, according to its graph was decreasing, then at x>-3, (-2,-1,0,1,..) the function increases.
3) Notice when x<-7, (x=-8, for example) the parabola is entirely over x-axis, then the graph for x <-7 is positive. And similarly, for x > 1, the function graph are over x-axis, then positive.