Explanation:
TRANSFORMATIONS:
Vertical shifts:
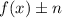 Shifts up/down n units
Shifts up/down n units
Horizontal shifts:
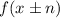 Shifts left/right n units
Shifts left/right n units
Reflection:
 Reflection over x-axis
Reflection over x-axis
Reflection:
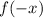 Reflection over y-axis
Reflection over y-axis
Dilation:
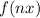
Dilation of x-coordinate n > 1 graph narrows; n < 1 graph widens
Dilation:
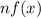
Dilation of y-coordinate n > 1 graph narrows; n < 1 graph widens.
=============================================================
We have:
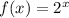
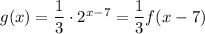
Dilation of y-coordinate (graph widens) and Shifts right 7 units.
look at the picture.