Question

looking at the graphs from f(x)=5^x and y=log5x, what can you say about the relationship between the functions

Answer 1

Reflection through y=x

Inverses

Explanation:

Let's look at the graphs.

I'm going to point out some interesting things about the graphs.

You will see that (a,b) is a point on f while (b,a) is a point on g.

I'm using that
`f(x)=5^x` while
`g(x)=\log_5(x)`.

You should see on the graph that:

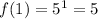`f(1)=5^1=5` while
`g(5)=\log_5(5)=1`

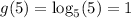
See that (1,5) is on f while (5,1) is on g.

Let's look at another point:

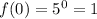`f(0)=5^0=1` while
`g(1)=\log_5(1)=0`

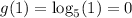
See that (0,1) is on f while (1,0) is on g.

This relationship that they have is that they are inverses.

In general, the inverse of
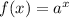`f(x)=a^x` is
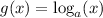`g(x)=\log_a(x)` and also vice versa.

Also visually, inverses when graphed will appear to be reflections through the y=x line.