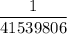Question

In one lottery, a player wins the jackpot by matching all five numbers drawn from white balls ( 1 through 45) and matching the number on the gold ballc( 1 through 34). If one ticket is purchased, what is the probability of winning the jackpot?

Answer 1

1 in 41,539,806.

Explanation:

The number of ways to pick 5 numbers from 45 = 45C5

= (45*44*43*42*41) / (5*4*3*2*1)

= 1,221,759.

There are 34 ways to pick a gold ball so total number of ways to get 6 matching numbers is

1221759*34

= 41,539,806.

Answer 2

Answer:
`(1)/(41539806)`

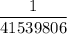
Explanation:

Given : Total white balls = 45

Number of correct balls needed to win = 5

Using combination ,

The total combination of getting 5 balls selected from 45 balls =
`^(45)C_5=`

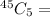
Total gold balls = 34

Similar;y , Number of ways to select 1 ball out of 34 =
`^(34)C_1`

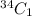
Total number of ways of selecting 5 white balls and 1 gold balls =
`^(45)C_5*^(34)C_1`

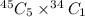
Using combination formula
`^nC_m=(n!)/(m!(n-m)!)`

`=(45*44*43*42*41*40!)/(120*40!)*(34!)/(1!(34-1)!)\\\\=1221759*34=41539806`

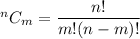
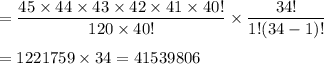
i.e. Total number of possible ways of selecting 5 white balls and 1 gold balls =41539806

But there is only one combination for wining the jackpot.

So the probability of winning the jackpot=
`\frac{\text{Favorable}}{\text{Total}}=(1)/(41539806)`

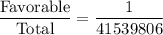
Hence, the required probability =
`(1)/(41539806)`