Answer:
Diverges; no sum
Explanation:
This is comparable to:
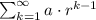 where:
where:
r is the common ratio and
 is the first term.
is the first term.
The series converges to:
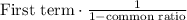
if the ratio's absolute value is less than 1.
This is a geometric series.
The common ration is -1.04 .
The first term in the series is 0.001.
Since the absolute value of -1.04 is 1.04>1, the series diverges.