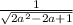Answer:
This is the one I referred to as Problem 3.
Explanation:
The length of OP is going to require a bit more work since we don't know P yet.
We need to find the equation for the line that travels through A & B.
Then we need to find the line that travels through O & P such that the choice in P makes OP perpendicular to AB. Perpendicular lines have opposite reciprocal slopes. The cool thing about OP is it is easy to identity the y-intercept. So the line for OP will just be
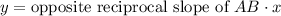 . Slope-intercept form is y=mx+b where m is the slope and b is the y-intercept.
. Slope-intercept form is y=mx+b where m is the slope and b is the y-intercept.
Let's go ahead and find the slope of AB.
The slope of AB can be found by using the formula:
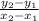 where
where
 and
and
 are points given to you on the line.
are points given to you on the line.
The points given to us are:
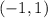 and
and

So entering these points into the formula gives us:
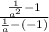
Simplifying:
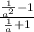
Clearing the mini-fractions by multiplying top and bottom by
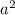 :
:
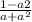 .
.
The top is a difference of squares and so can use formula
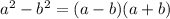 .
.
The bottom both terms have a common factor of
 so I can just factor that out of the two terms.
so I can just factor that out of the two terms.
Let's do that:
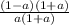
There is a common factor to cancel:
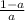
The slope of AB is
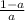 .
.
I'm going to use point-slope form to determine my linear equation for AB.
Point-slope form is
 where
where
 is slope and
is slope and
 is a point on the line that you know.
is a point on the line that you know.
So we have that (-1,1) is the point where
 is
is
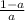 .
.
Plugging this in gives us:
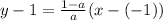
 .
.
So the linear equation that goes through points A and B is:
 .
.
Now we said earlier that the line for OP will be:
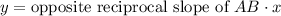 .
.
Opposite just means change the sign.
Reciprocal just means we are going to flip.
So the opposite reciprocal of
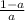 is:
is:
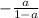 .
.
So the equation when graphed that goes through pts O & P is:
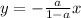 .
.
Now to actually find this point P, I need to find the intersection of the lines I have found. This lines I found for AB & OP respectively are:

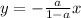
I'm going to use substitution to solve this system.
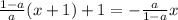
To solve this equation for x, I need to get the terms that contain x on one side while the terms not containing x on the opposing side.
I'm going to distribute the
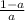 to both terms in the ( ) next to it:
to both terms in the ( ) next to it:
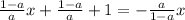
Now I'm to subtract
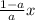 on both sides:
on both sides:
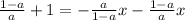
Factor out the x on the right hand side:
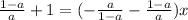
Now divide both sides by what x is being multiplied by:
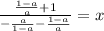
We need to clear the mini-fractions by multiplying top and bottom by
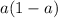 :
:
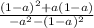
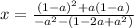
Distributing the - in front of the ( ) on bottom:
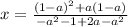
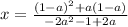
I'm going to factor the
 out on top since both of those terms have that as a common factor:
out on top since both of those terms have that as a common factor:
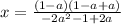
This simplify to:
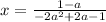
Now let's find the corresponding y-coord using either of one our equations.
I prefer the line for OP:
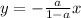 with
with
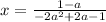
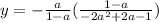
 's cancel:
's cancel:
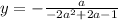
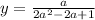 .
.
So point P is
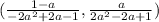 .
.
So now we can actually use the distance formula to compute the thing we called the height of the triangle which was the distance between O & P:
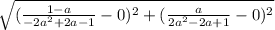
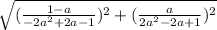

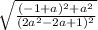
Let's simplify the top using
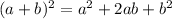 :
:

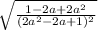
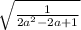 .
.