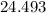Answer:
Confidence interval :
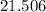 to
to
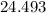
Explanation:
A quality analyst selects twenty racquets and obtains the following lengths:
21, 25, 23, 22, 24, 21, 25, 21, 23, 26, 21, 24, 22, 24, 23, 21, 21, 26, 23, 24
So, sample size = n =20
Now we are supposed to find Construct a 99.9% confidence interval for the mean length of all the junior's tennis racquets manufactured at this plant.
Since n < 30
So we will use t-distribution
Confidence level = 99.9%
Significance level = α = 0.001
Now calculate the sample mean
X=21, 25, 23, 22, 24, 21, 25, 21, 23, 26, 21, 24, 22, 24, 23, 21, 21, 26, 23, 24
Sample mean =
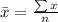
Sample mean =
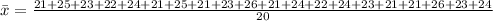
Sample mean =
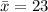
Sample standard deviation =
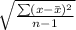
Sample standard deviation =
![\sqrt{((21-23)^2+(25-23)^2+(23-23)^2+(22-23)^2+(24-23)^2+(21-23)^2+(25-23)^2+(21-23)^2+(23-23)^2+(26-23)^2+(21-23)^2+(24-23)^2+(22-23)^2+(24-23)^2+(23-23)^2+(21-23)^2+(21-23)^2+(26-23)^2+(23-23)^2+(24-23)^2)/(20-1)}]()
Sample standard deviation= s =
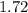
Degree of freedom = n-1 = 20-1 -19
Critical value of t using the t-distribution table
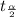 = 3.883
= 3.883
Formula of confidence interval :
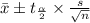
Substitute the values in the formula
Confidence interval :
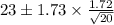
Confidence interval :
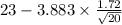 to
to
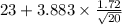
Confidence interval :
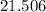 to
to
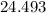
Hence Confidence interval :
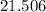 to
to