Question

A simple random sample of 58 adults is obtained from a normally distributed​ population, and each​ person's red blood cell count​ (in cells per​ microliter) is measured. The sample mean is 5.25 and the sample standard deviation is 0.52. Use a 0.01 significance level and the given calculator display to test the claim that the sample is from a population with a mean less than 5.4, which is a value often used for the upper limit of the range of normal values. What do the results suggest about the sample​ group?

Answer 1

Given : Sample mean = x = 5.25

Standard deviation = 0.52

To Find : Use a 0.01 significance level and the given calculator display to test the claim that the sample is from a population with a mean less than 5.4

Solution:

Sample size = n = 58

Hypothesis :
`H_0:\mu = 5.4\\H_a:\mu<5.4`

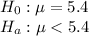
Test statistic:
`z =\frac {x-\mu}{\frac {s}{√(n)}}`

x = 5.25

μ = 5.4

s = 0.52

n = 58

Substitute the values :

`z =(5.25-5.4)/((0.52)/(√(58)))`

`z =−2.196`

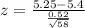
Refer the p value using z table

P-value = P(z ≤ -2.196) = 0.0143

As P-value > 0.01,

So, we accept the null hypothesis

Conclusion: There is significant statistical evidence to conclude that the claim that the sample is from a population with a mean less than 5.4 is False at alpha = 0.01, the level of significance.