Answer: The amount of energy released in the process is 4.042 MeV.
Step-by-step explanation:
The chemical reaction for the fusion of deuterium nucleus follows the equation:
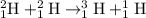
Atomic mass of the nucleus also contains some mass of the electrons.
Mass of electron in
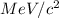 is
is
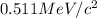
- Calculating the mass of deuterium nucleus:
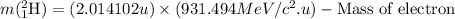
So, initial mass of the reaction =
![2[(1876.124MeV/c^2)-(0.511MeV/c^2)]=3751.226MeV/c^2](https://img.qammunity.org/2020/formulas/physics/college/xlio1m16os712dkp4cl1p338fstvd1upbj.png)
- Calculating the mass of tritium nucleus:
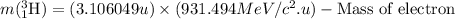
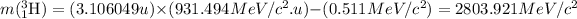
So, final mass of the reaction =
![2803.921-[(1.007267u* 931.494MeV/c^2.u)]=3747.184](https://img.qammunity.org/2020/formulas/physics/college/5q2xundckkaozw34mqjpttzit5henyl7yc.png)
Difference between the masses of the nucleus:
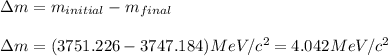
Energy released in the process is calculated by using Einstein's equation, which is:

Putting value of
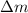 in above equation, we get:
in above equation, we get:

Hence, the amount of energy released in the process is 4.042 MeV.