Question

A simple pendulum consists of a ball connected to one end of a thin brass wire. The period of the pendulum "is 2.51 s". The temperature rises by 142 C°, and the length of the wire increases. Determine the change in the period of the heated pendulum.

Answer 1

0.0034 sec

Step-by-step explanation:

L = initial length

T = initial time period = 2.51 s

Time period is given as

`T = 2\pi \sqrt{(L)/(g)}`

`2.51 = 2\pi \sqrt{(L)/(9.8)}`

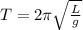
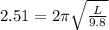
L = 1.56392 m

L' = new length

ΔT = Rise in temperature = 142 °C

α = coefficient of linear expansion = 19 x 10⁻⁶ °C

New length due to rise of temperature is given as

L' = L + LαΔT

L' = 1.56392 + (1.56392) (19 x 10⁻⁶) (142)

L' = 1.56814 m

T' = New time period

New time period is given as

`T' = 2\pi \sqrt{(L')/(g)}`

`T' = 2\pi \sqrt{(1.56814)/(9.8)}`

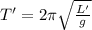
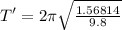
T' = 2.5134 sec

Change in time period is given as

ΔT = T' - T

ΔT = 2.5134 - 2.51

ΔT = 0.0034 sec