Answer: There are 70 houses that have exactly two of these amenities.
Explanation:
Number of house in a certain development = 150
Number of houses have air conditioning n(A)=
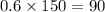
Number of houses have sunporch n(B) =
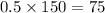
Number of houses have swimming pool n(C) =

Number of houses have all three amenities = 5
Number of houses have none of them = 5
So, remaining houses = 150-5=145
As we know the rule of sets:
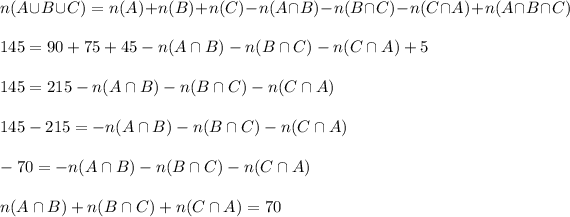
Hence, there are 70 houses that have exactly two of these amenities.