Answer:
The value of x is 12
Explanation:
Let ABC is a triangle in which,
AB = x, BD = 9 unit, DC = 7 unit,
Where, D ∈ BC,
∵ ∠ABC ≅ ∠DBC ( common angles )
Also, ∠BAC ≅ ∠ADB ( right angles )
By AA similarity postulate,
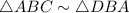
∵ Corresponding sides of similar triangles are in same proportion,
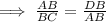
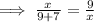 ( ∵ BC = BC + DC )
( ∵ BC = BC + DC )
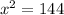
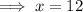 ( Sides can not be negative )
( Sides can not be negative )
Hence, the value of x is 12.