Question

Solve for x.

Answers available are.
a.) 12.5
b.) 4√7
c.) 3√7
d.) 12

Answer 1

The value of x is 12

Explanation:

Let ABC is a triangle in which,

AB = x, BD = 9 unit, DC = 7 unit,

Where, D ∈ BC,

∵ ∠ABC ≅ ∠DBC ( common angles )

Also, ∠BAC ≅ ∠ADB ( right angles )

By AA similarity postulate,

`\triangle ABC\sim \triangle DBA`

∵ Corresponding sides of similar triangles are in same proportion,

`\implies (AB)/(BC)=(DB)/(AB)`

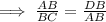
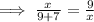`\implies (x)/(9+7)=(9)/(x)` ( ∵ BC = BC + DC )

`x^2 = 144`

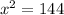
`\implies x = 12` ( Sides can not be negative )

Hence, the value of x is 12.

Answer 2

d) 12

Explanation:

Given:

Right triangle with side 9+7=16

let the third side of bigger triangle be y

and perpendicular line between 9 and 7 be z

Now:

By Pythagoras theorem:

(16)^2=x^2+y^2

x^2=256-y^2

Also

y^2=z^2 +7^2

z^2=y^2-49

and

x^2=9^2 + z^2

Now substituting z^2=y^2-49 in above we get:

x^2=81 + y^2-49

x^2=32+y^2

Adding x^2=256-y^2 and x^2=32+y^2 we get:

2x^2= 288

x^2=144

x=12 !