Question

A body which has surface area 5cm² and temperature of 727°C radiates 300J of energy in one minute. Calculate it's emissivity given that Stefan Boltzmann constant = 5.67 × 10^8W^-8m^-8K^-4

Answer 1

Answer: 0.17

Step-by-step explanation:

The Stefan-Boltzmann law establishes that a black body (an ideal body that absorbs or emits all the radiation that incides on it) "emits thermal radiation with a total hemispheric emissive power proportional to the fourth power of its temperature":

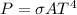`P=\sigma A T^(4)` (1)

Where:

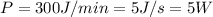`P=300J/min=5J/s=5W` is the energy radiated by a blackbody radiator per second, per unit area (in Watts). Knowing
`1W=(1Joule)/(second)=1(J)/(s)`

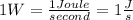
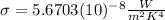`\sigma=5.6703(10)^(-8)(W)/(m^(2) K^(4))` is the Stefan-Boltzmann's constant.

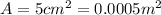`A=5cm^(2)=0.0005m^(2)` is the Surface area of the body

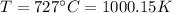`T=727\°C=1000.15K` is the effective temperature of the body (its surface absolute temperature) in Kelvin.

However, there is no ideal black body (ideal radiator) although the radiation of stars like our Sun is quite close. So, in the case of this body, we will use the Stefan-Boltzmann law for real radiator bodies:

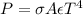`P=\sigma A \epsilon T^(4)` (2)

Where
`\epsilon` is the body's emissivity

(the value we want to find)

Isolating
`\epsilon` from (2):

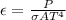`\epsilon=(P)/(\sigma A T^(4))` (3)

Solving:

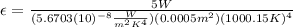`\epsilon=(5W)/((5.6703(10)^(-8)(W)/(m^(2) K^(4)))(0.0005m^(2))(1000.15K)^(4))` (4)

Finally:

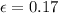`\epsilon=0.17` (5) This is the body's emissivity