Answer:
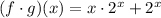
Now if you meant to have an open circle that would lead to a totally different answer. So if that is the case, I need to know. Thank you kindly.
Explanation:
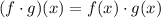
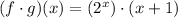 (Plugging in the given expressions)
(Plugging in the given expressions)
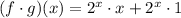 (By distributive property)
(By distributive property)
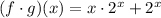 (By commutative and identity property)
(By commutative and identity property)