Step-by-step explanation:
As it is given that
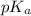 = 4.20 and pH is 4.0.
= 4.20 and pH is 4.0.
Now, we use Henderson-Hasslbach equation as follows.
pH =
![pK_(a) + log ([salt])/(acid)](https://img.qammunity.org/2020/formulas/chemistry/college/2nm8pur7svwnmo1hpco9dbwea0wdlk2v8e.png)
So, it is given that salt is sodium benzoate and acid is benzoic acid. Hence, the given equation will become as follows.
pH =
![pK_(a) + log \frac{[\text{sodium benzoate}]}{\text{[benzoic acid]}}](https://img.qammunity.org/2020/formulas/chemistry/college/n7aah6gp2uekwiy84kwerorawkmks8tbmo.png) ........ (1)
........ (1)
Now, substitute the given values into equation (1) as follows.
pH =
![pK_(a) + log \frac{[\text{sodium benzoate}]}{\text{[benzoic acid]}}](https://img.qammunity.org/2020/formulas/chemistry/college/n7aah6gp2uekwiy84kwerorawkmks8tbmo.png)
4.0 =
![4.20 + log \frac{[{C_(6)H_(5)COONa}]}{[C_(6)H_(5)COOH]}](https://img.qammunity.org/2020/formulas/chemistry/college/aibeoctw1v6jedwjombev5w413zrvyt7ji.png)
![log \frac{[{C_(6)H_(5)COONa}]}{[C_(6)H_(5)COOH]}](https://img.qammunity.org/2020/formulas/chemistry/college/cfvyqffv66wip2oqfc4cb6ykaosin8wctf.png) = 4.0 - 4.20
= 4.0 - 4.20
= - 0.20
![\frac{[{C_(6)H_(5)COONa}]}{[C_(6)H_(5)COOH]}](https://img.qammunity.org/2020/formulas/chemistry/college/64yv6lppjzrurijjzxopdihht8k8m7qfh7.png) =
=

= 0.613
or,
![[C_(6)H_(5)COONa]](https://img.qammunity.org/2020/formulas/chemistry/college/al9o4i4c1erjessuvrg86vwskyb2puij17.png) =
=
![0.613 * [C_(6)H_(5)COOH]](https://img.qammunity.org/2020/formulas/chemistry/college/evqyu49m2w0kuljp467a7eltathizbn2kl.png) ............. (2)
............. (2)
Since, the total volume of (acid + base) is given as 100.0 mL. So, let us assume volume of acid is x and volume of base is y.
Hence, x + y = 100 mL ....... (3)
And, equation (2) will become as follows.
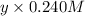 =
=
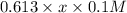
y = 0.255x
Substituting value of y into equation (3) as follows.
x + 0.255x = 100 mL
1.255 x = 100 mL
x = 79.68 mL
So, value of y will be as follows.
y = 0.255 x
= 0.255 × 79.68 mL
= 20.31 mL
Thus, we can conclude that volume of benzoic acid is 79.68 mL and volume of sodium benzoate is 20.31 mL.